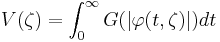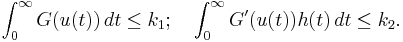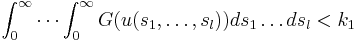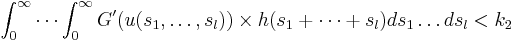Massera's lemma
In stability theory and nonlinear control, Massera's lemma, named after José Luis Massera, deals with the construction of the Lyapunov function to prove the stability of a dynamical system.[1] The lemma appears in (Massera 1949, p. 716) as the first lemma in section 12, and in more general form in (Massera 1956, p. 195) as lemma 2. In 2004, Massera's original lemma for single variable functions was extended to the multivariable case, and the resulting lemma was used to prove the stability of switched dynamical systems, where a common Lyapunov function describes the stability of multiple modes and switching signals.
Contents |
Massera's original lemma
Massera’s lemma is used in the construction of a converse Lyapunov function of the following form (also known as the integral construction)
for an asymptotically stable dynamical system whose stable trajectory starting from 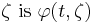
The lemma states:
Let
be a positive, continuous, strictly decreasing function with
as
. Let
be a positive, continuous, nondecreasing function. Then there exists a function
such that
and its derivative
are class-K functions defined for all t ≥ 0
- There exist positive constants k1, k2, such that for any continuous function u satisfying 0 ≤ u(t) ≤ g(t) for all t ≥ 0,
Extension to multivariable functions
Massera's lemma for single variable functions was extended to the multivariable case by Vu and Liberzon.[2]
Let
be a positive, continuous, strictly decreasing function with
as
. Let
be a positive, continuous, nondecreasing function. Then there exists a differentiable function
such that
and its derivative
are class-K functions on
.
- For every positive integer
, there exist positive constants k1, k2, such that for any continuous function
satisfying
we have
for all
,
References
- Massera, José Luis (1949), "On Liapounoff's conditions of stability", Annals of Mathematics. Second Series (Annals of Mathematics) 50 (3): 705–721, doi:10.2307/1969558, JSTOR 1969558, MR0035354
- Massera, José Luis (1956), "Contributions to stability theory", Annals of Mathematics. Second Series (Annals of Mathematics) 64 (1): 182–206, doi:10.2307/1969955, JSTOR 1969955, MR0079179
- Massera, José Luis; Schäffer, Juan Jorge (1966), Linear differential equations and function spaces, Pure and Applied Mathematics, Vol. 21, Boston, MA: Academic Press, MR0212324
Footnotes
- ^ Khalil, H.K. (2001), Nonlinear Systems, Prentice Hall, ISBN 0130673897
- ^ Vu, L.; Liberzon, D. (2005), "Common Lyapunov functions for families of commuting nonlinear systems", Systems & Control Letters 54 (5): 405–416, doi:10.1016/j.sysconle.2004.09.006, http://linkinghub.elsevier.com/retrieve/pii/S0167691104001598, retrieved 2008-07-18.